待ち行列
待ち行列とはサービスを提供するシステムの混雑状況を分析するための理論であり、建築計画分野では、室数、窓口数、便器数の設定など規模計画に関する応用範囲がある。1909年のアーラン(E.K. Erlang)による電話回線の混み合い問題の研究が最初であるとされている。
1.待ち行列の原理
- 混雑状況
- サービスを提供できる能力には限界がある。
- サービスを受ける側(客)はランダムにやってくる。
- サービス時間もランダムである。
- 待ち行列モデルの構成要素
- 客の到着の仕方(X)
- サービス時間(Y)
- サービスを提供する側(サーバー)の数(s)
- ケンドールの記号
- X:客の到着の仕方 →ポアソン到着
- Y:サービス時間 →指数サービス
- ポアソン到着(M): ランダムな到着をモデル化したもの。
- 指数サービス(M): サービス時間をモデル化したもの。
- 待ち行列モデルの評価量
- 平均待ち時間: 客が待った時間の平均
- 平均滞在時間: 客がシステム内に滞在した時間の平均
- 平均待ち客数: 待っている客数の平均
- 平均系内客数: システム内に滞在している客数の平均
- あふれ率: 待ち室がいっぱいでシステム内に入ることを拒否された客の割合
- M|M|sモデル
利用が集中するとサービスを受けられない客が発生し、待ちが生じる。待ちが過剰に生じないように計画するのが規模計画の目的である。
待ち行列モデルは X|Y|s の形式で表記する。
の場合、M|M|s と表記する。
λ=到着率(単位時間当りの到着客数:人/時間) 1/λ=平均到着時間
μ=サービス率(人/時間) 1/μ平均サービス時間 s=サーバー数
とすると評価量は次の関係で示される。
![]()
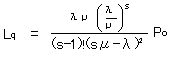
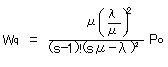
![]()
参考文献:例解OR小和田正・加藤豊 実教出版
2.建築分野における例
[例1] 単純なモデル
ある病院の採血室の台数を計画する。採血を行う時間は9:00~12:00、採血患者数は1日当り500人、採血に要する時間は1人当り2分である。M|M|sモデルと考え、台数を6とした時、次の各数値が求められる。
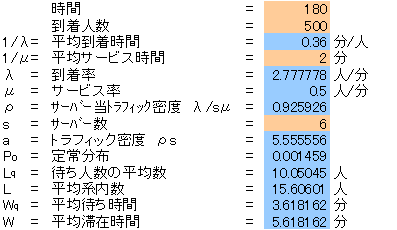
なおS=7ではWqは0.65分、S=5では非定常(客がどんどん溜まっていく状態)となる。台数は6台が最低限必要と考えられる。
[例2] 複合したモデルb
ある病院の内科系診察数、外待合の待合滞留人数を計画する。1日平均外来患者数2000人、内科の比率35%、初診率8%とする。平均診察時間は初診15分、再診5分、受付時間8:30~11:30、診察開始時刻9:00、診察終了時間は13:00頃までを限度とする。再診予約率98%、付き添い率は30%とする。
- 1日の内科外来初診患者数は2000人×35%×8%=56人/日
診察時間は9:00~13:00で4時間、15分/人とすれば平均16人/室で56/16=3.5室あれば足りる計算となる。 - M|M|sモデルとすると4室で以下のような待ち時間となる。(3室では非定常)
- 再診患者は予約時間30分前に到着するとすると、最大で
系内最大滞留患者数=診察室数×30分当りに診察を受ける患者数×2 となる。診察室数をnとすると 系内最大滞留患者数(L1)=n×(30分/5分)×2=12n人、外待ち最大滞留患者数(L2)=12n-n-n=10n となる。
診察室数(n)を8室とするとL1=96人、L2=80人となる。 - 以上から初診4室、再診8室とすると外待合の滞留は6.66+80≒87人、付き添い率を考慮して113人程度の外待ちが必要ということになる。

平均系内数は8.66人であり診察室1人、中待合1人がいるとすると8.66-1-1=6.66人が外待合にいることになる。
現実の計画に際しては診察時間に変動があり予約(再診)患者の滞留が一様でないことを考慮する必要がある。同時に患者サービスの視点からも運用・施設を考える必要があることを付け加える。