重回帰分析

２つ以上の説明変量から目的変量を推定する方法。この場合の相関・回帰に当るものを重相関・重回帰といい、回帰分析に当るものを重相関分析という。また多くの変量の中でどの要素間に相関が見られるのかを知ることも建築分野では重要である。

1. 重相関

変量ｘ１，ｘ２・・・ｘｎの各々の相関を求め表形式にまとめる（例：表1）。これを行列で示したものは相関行列という。


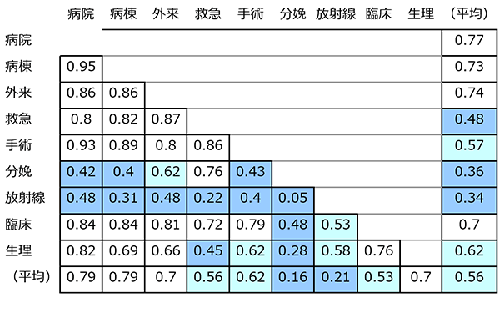
※一般には有意水準0.01（高度に有意）を**、有意水準0.05（有意）を*で表す。　表1

2. 回帰方程式

変量ｎからなる方程式は次式で表され、これを回帰方程式という。またa1･･･anは偏回帰係数、あるいは単に係数と呼ぶ。
ｙ＝a1x1+a2x2+･･･+anxn+a0　　（式1）
また説明変数が目的変数に及ぼす影響を知りたい時、偏回帰係数間の直接比較ができないため、偏回帰係数を標準化（平均0、分散1）し比較する。このことにより説明変数の目的変数への影響力の大きさを知ることができる。
偏回帰係数は次の式を満たす。左辺左側の行列は分散･共分散行列を示す。




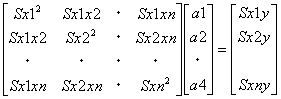
また偏回帰係数はmicrosoft　Exel　ではツール＞分析ツール＞回帰分析　でウイザード形式で、またLINEST関数で回帰方程式を求めることができる。



3. 評価

回帰方程式で求められる予測値と実際のｙ値の相関係数を重相関係数（＝R)といい、この値が1に近いほど現実をよく表していることになる。またR²を決定係数という。

4. 偏相関係数

２変量の相関を見るとき、各々が第３の変量の影響を受け見かけ上の相関を示すことがある。このような第３の変量の影響を取り除いた相関を偏相関係数という。

２．建築分野における例

［例１］ 以下に１４病院A～Ｎの部門別面積を示す。部門は9部門とした。これら以外の部門は挙げていないため、９部門の合計は病院（全体）面積ではない。



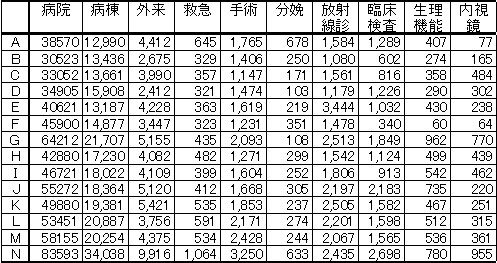
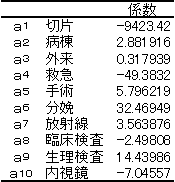
この表から病院（全体）面積を目的変量として重回帰分析を行い右の係数（偏回帰係数）が得られた。計算にはＥｘｅｌ　分析ツールを使用した。
この結果から病院（全体）面積（目的変量）ｙは（式1）　ｙ＝a1x1+a2x2+･･･+anxn+a0　の式でａ0～a10　に右表の値を代入したものとなる。
重相関係数（Ｒ）は0.983235、決定係数（Ｒ^２）は0.966751であった。
また表１は部門別面積間の相関を見たものである。この表からは、病院内の部門別面積構成において、救急、分娩・放射線（診断）と他部門との関連は低く、生理機能検査・内視鏡はやや低いということができる。